Schriftliche Rechenverfahren – was ist das?

In diesem Blogbeitrag geben wir einen Überblick über die Rechenverfahren der 4 Grundrechenarten und ihren Hintergrund und erklären, wie man sie im Worksheet Crafter nutzt.

Heute möchte ich einen Abstecher in die Rechenverfahren für die vier Grundrechenarten machen – und im Anschluss das Feld für schriftliche Rechenverfahren erkunden, mit dem Sie als Lehrkraft im Worksheet Crafter selbst komplexe Matheaufgaben ganz einfach in Ihre Arbeitsblätter inkorporieren können.

Der Worksheet Crafter ist eine ansprechende und einfach zu bedienende Software für die differenzierte Lernmaterialgestaltung in Grund-, Volks- und Förderschule. Wer mehr wissen möchte, klickt einfach hier.

Die schriftlichen Rechenverfahren in den Worksheet Crafter einzubinden, war keine kleine Herausforderung, da uns dazu von unseren Nutzer*innen viele unterschiedliche Wünsche und Anforderungen genannt wurden. Aber bevor wir uns den vielen Tricks und Kniffen zuwenden, die hier im Worksheet Crafter möglich sind, ein kurzer Blick auf die Rechenverfahren im Allgemeinen.

Rechenverfahren – Algorithmen mit Stift und Papier

Die Grundrechenarten (manchmal auch kurz: schlicht Rechenarten) sind, wie wir alle wissen, die vier mathematischen Operationen

• Addition (Plusrechnen)

• Subtraktion (Minusrechnen)

• Multiplikation (Malnehmen)

• Division (Teilen).

Ihre Beherrschung gehört neben dem Lesen und Schreiben zu den Grundfertigkeiten, die Kinder während ihrer Schulzeit erwerben sollten und im Leben brauchen.

Wenn es um kleine Zahlen und Zahlräume geht, können die Grundrechenarten von den meisten Kindern (und Erwachsenen) problemlos im Kopf durchgeführt werden. Sobald aber größere Zahlen verrechnet werden sollen, braucht es oft eine Krücke – und die bieten die schriftlichen Rechenverfahren, häufig einfach als „Rechenverfahren“ bezeichnet.

Die schriftlichen Rechenverfahren bieten eine einfache Möglichkeit, Zahlen miteinander zu verrechnen, ohne, dass ein Taschenrechner zur Hand ist. Davon profitieren auch Kinder, denen das Rechnen nicht so leichtfällt: Wo sie Ergebnisse vorher mühsam durch Zählen ermitteln mussten, können sie die Aufgabe nun anhand klarer, einfacher Regeln in Teilstücke zerlegen und lösen.

Anders ausgedrückt: Die Ergebnisse werden über Algorithmen ermittelt – wenn auch auf Stift und Papier und nicht im Inneren eines gigantischen Rechenzentrums. :-)

Durch die schriftlichen Rechenverfahren braucht es kein Nachdenken mehr über die Aufgabe – gemäß der festgelegten Regeln kann einfach das Ergebnis ermittelt werden. Das ist der Nachteil, den manche an den schriftlichen Rechenverfahren sehen. Rechnen nach Schema F könne dazu führen, dass der Blick für die Beziehungen und Größe der Zahlen verloren geht.

Rechenverfahren zur schriftlichen Addition

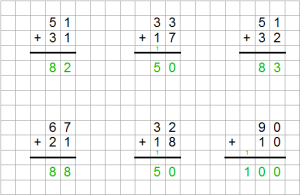
1. Bei der schriftlichen Addition werden die Summanden stellengerecht untereinander geschrieben.

2. Die Ziffern innerhalb eines Stellenwerts, die untereinander stehen, werden dann jeweils separat zusammengerechnet. Man beginnt dabei immer mit dem kleinsten Stellenwert, also von rechts nach links.

3. Die Summe der Teilrechnungen muss stellengerecht in der entsprechenden Spalte unter dem Strich notiert werden. Wenn das Teilergebnis zweistellig ist, wird nur der Wert des Einers im Ergebnis notiert. Die übrigen 10 Einheiten des Teilergebnisses werden dann als Übertrag beim nächstgrößeren Stellenwert vermerkt.

4. Dieser Übertrag wird im darauffolgenden Rechenschritt zu dem nächsten Teilergebnis addiert.

5. Das Gesamtergebnis ist nach der letzten Teilrechnung direkt unter dem Strich ablesbar.

Rechenverfahren zur schriftlichen Subtraktion

1. Auch bei der schriftlichen Subtraktion werden beide Zahlen stellengerecht untereinander geschrieben.

2. Wieder beginnt man von rechts, nur dass diesmal die Ziffern des Subtrahenden von denen des Minuenden abgezogen werden.

3. Die Differenz wird in der passenden Spalte unter dem Strich notiert.

4. Auch hier wird ein „Übertrag“ nötig, nämlich, wenn eine der Ziffern kleiner als die andere ist.

5. Durch die stellengerechte Notation der Teilergebnisse kann das Gesamtergebnis direkt abgelesen werden.

Rechenverfahren zur schriftlichen Multiplikation

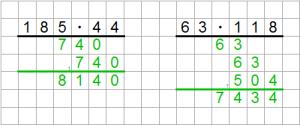
1. Bei der schriftlichen Multiplikation werden die Faktoren nebeneinander notiert, nicht untereinander.

2. Danach wird jede Ziffer des zweiten Faktors mit jeder Ziffer des ersten Faktors multipliziert.

3. Man beginnt mit der Multiplikation des größten Stellenwerts des zweiten Faktors mit der Einerstelle des ersten Faktors.

4. Die Teilprodukte werden entsprechend ihrer Stellenwerte unter dem zweiten Faktor angeordnet. Dadurch muss nur im kleinen Einmaleins gerechnet werden.

5. Danach fährt man mit dem nächstkleineren Stellenwert des zweiten Faktors fort. Dieser wird mit jeder Stelle des ersten Faktors multipliziert.

6. Auch diese Ergebnisse werden in der nächsten Zeile notiert. Mögliche Überträge werden stellengerecht im Kopf behalten.

7. Zuletzt müssen die Teilergebnisse addiert werden.

Rechenverfahren zur schriftlichen Division

1. Bei der schriftlichen Division wird die Divisionsaufgabe zunächst normal nebeneinander aufgeschrieben.

2. Wir rechnen jetzt allerdings anders als bei den anderen drei Operationen und beginnen mit dem größten Stellenwert des Dividenden.

3. Ausgehend von diesem Stellenwert prüfen wir, welches das größte Vielfache des Divisors ist, das in die einzelnen Stellenwerte passt.

4. Dies wird stellengerecht darunter notiert.

5. Weil manche Stellenwerte dabei nicht komplett verrechnet werden können, muss deren Differenz in der nächsten Teilrechnung berücksichtigt werden, und so weiter.

Schriftliche Rechenverfahren im Worksheet Crafter

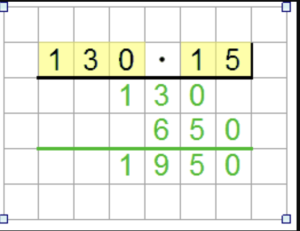
Mit dem Feld für schriftlichen Rechenverfahren lassen sich im Worksheet Crafter schriftliche Aufgaben für alle vier Grundrechenarten erstellen. Der Worksheet Crafter berechnet hierbei automatisch die Lösung  und zeigt diese mitsamt den Zwischenschritten und Überträgen an. Hier ist ein Beispiel für zwei Multiplikationsaufgaben:

Flexible Auswahl des Zahlenraums

Der gewünschte Zahlenraum lässt sich bei Verwendung des Aufgabengenerators wieder direkt bei der Aufgabe einstellen. Für die schriftlichen Rechenverfahren habe ich mir jedoch noch etwas Besonderes ausgedacht: für jede Aufgabenzahl lässt sich anhand einer einfachen Formel exakt festlegen, wie die Zahl aufgebaut sein darf:

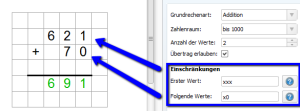
Was auf den ersten Blick kompliziert aussieht, ist eigentlich ganz einfach. Ein "x" steht für eine beliebige Zahl, während eine "0" für eine Null steht. Im obigen Beispiel habe ich somit festgelegt, dass die erste Zahl eine beliebig dreistellige Zahl sein darf (z.B. 621). Die zweite Zahl wiederum muss zweistellig sein und mit einer 0 enden, d.h. eine Zehnerzahl sein (z.B. 70). Auf diese Art und Weise kann ich sehr flexibel mein Zahlenmaterial eingrenzen.

Übertrag und Rest

Es gibt noch weitere Einstellungen, die den Zahlenraum zusätzlich eingrenzen:

Für Additions- und Subtraktionsaufgaben kann ich mit einem Häkchen festlegen, ob Überträge erlaubt sind. Wenn dieses Häkchen nicht gesetzt ist, dann enthalten die Aufgaben keinerlei Zehnerübergänge, Hundererübergänge usw. Für Divisionsaufgaben wiederum lässt sich definieren, ob die Lösung einen Rest enthalten darf.

Aufgaben mit mehr als zwei Summanden/Minuenden

Additions- und Subtraktionsaufgaben können auf Wunsch auch mehr als zwei Summanden bzw. Minuenden enthalten. Hierfür gibt es eine entsprechende Einstellung in den Eigenschaften des Feldes:

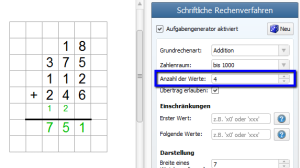
Hierbei können Sie selbst angeben, ob das Rechenzeichen vor allen Zahlen oder nur vor der letzten Zahl angezeigt werden soll.

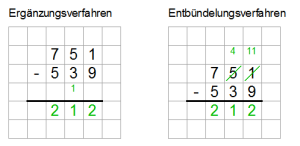
Unterstützung für beide Subtraktions-Verfahren

Da Mathematik ja überall gleich ist :-), gibt es netterweise zwei verschiedene Verfahren, die Übertrage bei Subtraktionsaufgaben darzustellen: das Ergänzungsverfahren und das Entbündelungsverfahren. Der Worksheet Crafter unterstützt beide Verfahren:

Manueller Modus mit Lösungen

Bei den schriftlichen Rechenverfahren können im manuellen Modus, d.h. bei deaktiviertem Aufgabengenerator, die Zahlen selbst eingetragen werden, so dass ganz gezielt Aufgaben erstellt werden können. Dabei berechnet der Worksheet Crafter auch hierbei automatisch die Lösung und zeigt sie mitsamt Zwischenrechnungen und Überträgen an. Hier ist ein kleines Beispiel, wie das in der Praxis bei der Eingabe aussieht:

Auf diese Art und Weise können auch "von Hand" erstellte Aufgaben zusammen mit Selbstkontrollen verwendet und mitsamt Lösungen ausgedruckt werden.

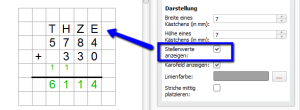
Optionale Anzeige der Stellenwerte

Für Additions- und Subtraktionsaufgaben lassen sich, falls gewünscht, oberhalb der Aufgabe die Stellenwerte einblenden:

Optionales Ausblenden der Rechenkästchen

Die Rechenkästchen können bei den schriftlichen Rechenverfahren nach Belieben angezeigt oder auch ausgeblendet werden. Die Größe der Rechenkästchen ist hierbei frei einstellbar:

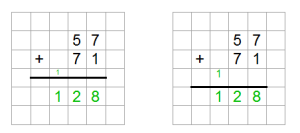
Flexible Position der Summe-Striche

Einige KundInnen sagten mir, dass die Striche unbedingt mittig in den Zeilen platziert sein sollten. Andere KundInnen wiederum meinten, dass die Striche genau auf den Rechenkästchen-Linien liegen müssen. Daher lässt sich bei den schriftlichen Rechenverfahren im Worksheet Crafter beides umsetzen:

Mehrere Aufgaben durch einfaches Vergrößern hinzufügen

Und zu guter Letzt gilt für die schriftlichen Rechenverfahren dasselbe wie für die schon vorhandenen Rechenpäckchen: falls Sie mehrere Aufgaben wünschen, dann können Sie einfach das Feld vergrößern. Der Worksheet Crafter füllt den zusätzlichen Platz automatisch mit weiteren Aufgaben aus. Hier ist ein Beispiel:

Und, was meinen Sie?

Das war die kleine Einführung. Was halten Sie davon? Vermutlich können wir mit dem Worksheet Crafter niemals alle Wünsche zu den Rechenverfahren erfüllen – das Thema ist einfach sehr komplex. Ich hoffe jedoch, dass Ihnen das Feld gefällt und Sie Lust auf den Worksheet Crafter bekommen. Über Rückmeldung in den Kommentaren würde ich mich riesig freuen.

Liebe Grüße,
Fabian Röken